Графическое решение уравнений, неравенств, систем с параметром (алгебра и начала анализа) Оглавление

I. Введение

II. Уравнения с параметрами.

§ 1. Определения.

§ 2. Алгоритм решения.

§ 3. Примеры.

III. Неравенства с параметрами.

§ 1. Определения.

§ 2. Алгоритм решения.

§ 3. Примеры.

IV. Список литературы.

Введение

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.

Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.

В моём реферате рассмотрены часто встречающиеся типы уравнений, неравенств и их систем, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов и при поступлении а ВУЗ.

§ 1. Основные определения

Рассмотрим уравнение

¦ (a, b, c, …, k , x)=j (a, b, c, …, k , x), (1)

где a, b, c, …, k , x -переменные величины.

Любая система значений переменных

а = а0, b = b0, c = c0, …, k = k0, x = x0,

при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k , x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аÎ А, bÎ B, …, xÎ X. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.

Переменные a, b, c, …, k , которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.

Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k , l, m, n а неизвестные – буквами x, y,z.

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

Два уравнения, содержащие одни и те же параметры, называются равносильными, если:

а) они имеют смысл при одних и тех же значениях параметров;

б) каждое решение первого уравнения является решением второго и наоборот.

§ 2. Алгоритм решения. Находим область определения уравнения. Выражаем a как функцию от х. В системе координат хОа строим график функции а=¦ (х) для тех значений х, которые входят в область определения данного уравнения.

Находим точки пересечения прямой а=с, где сÎ (-¥ ;+¥) с графиком функции а=¦ (х).Если прямая а=с пересекает график а=¦ (х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦ (х) относительно х.

Записываем ответ. § 3. Примеры

I. Решить уравнение

Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а:

или

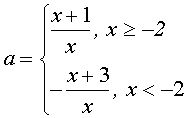
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.

Если а Î (-¥ ;-1]È (1;+¥)È , то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения относительно х.

Таким образом, на этом промежутке уравнение (1) имеет решение .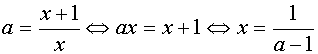

Если а Î , то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений и 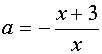, получаем

И .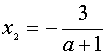

Если а Î , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.

Если а Î (-¥ ;-1]È (1;+¥)È , то ;

Если а Î , то , ;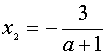

Если а Î , то решений нет.

II. Найти все значения параметра а, при которых уравнение имеет три различных корня.

Переписав уравнение в виде и рассмотрев пару функций , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции , при которых он имеет точно три точки пересечения с графиком функции .

В системе координат хОу построим график функции ). Для этого можно представить её в виде и, рассмотрев четыре возникающих случая, запишем эту функцию в виде

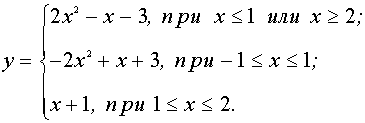
Поскольку график функции – это прямая, имеющая угол наклона к оси Ох, равный , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции . Поэтому находим производную

III. Найти все значения параметра а, при каждом из которых система уравнений

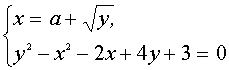
имеет решения.

Из первого уравнения системы получим при Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы “скользят” вершинами по оси абсцисс.

Выделим в левой части второго уравнения полные квадраты и разложим её на множители

Множеством точек плоскости , удовлетворяющих второму уравнению, являются две прямые

Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.

Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается

прямой ), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то .

Случай касания “полупараболы” с прямой определим из условия существования единственного решения системы

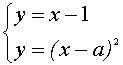
В этом случае уравнение

имеет один корень, откуда находим:

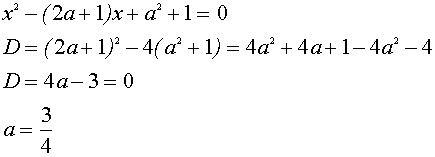
Следовательно, исходная система не имеет решений при , а при или имеет хотя бы одно решение.

Ответ: а Î (-¥ ;-3] È (;+¥).

IV. Решить уравнение

Использовав равенство , заданное уравнение перепишем в виде

Это уравнение равносильно системе

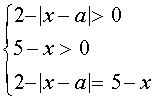
Уравнение перепишем в виде

. (*)

Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций и Из графика следует, что при графики не пересекаются и, следовательно, уравнение не имеет решений.

Если , то при графики функций совпадают и, следовательно, все значения являются решениями уравнения (*).

При графики пересекаются в одной точке, абсцисса которой . Таким образом, при уравнение (*) имеет единственное решение - .

Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям

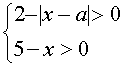
Пусть , тогда . Система примет вид

Её решением будет промежуток хÎ (1;5). Учитывая, что , можно заключить, что при исходному уравнению удовлетворяют все значения х из промежутка , где х 1 и х 2 – абсциссы точек пересечения графиков, будет решением исходно­го неравенства..gif" width="68 height=47" height="47">, то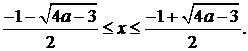

Когда «полупарабола» и прямая пересекаются только в одной точке (это соответствует случаю а > 1), то решением будет отрезок [-а ; х 2"], где х 2" – больший из корней х 1 и х 2 (положение IV).

Пример 4 ..gif" width="85" height="29 src=">.gif" width="75" height="20 src=">. Отсюда получаем .

Рассмотрим функции и . Среди них лишь одна задает семейство кривых. Теперь мы видим, что произведенная замена приносит несомненную пользу. Парал­лельно отметим, что в предыдущей задаче аналогичной заменой можно заставить двигаться не «полупараболу», а прямую. Обратимся к рис. 4. Очевидно, если абсцисса вершины «полупараболы» больше единицы, т. е. –3а > 1, , то уравнение корней не имеет..gif" width="89" height="29"> и име­ют разный характер моно­тонности.

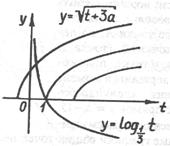
Ответ. Если то уравнение имеет один корень; если http://pandia.ru/text/78/074/images/image039_10.gif" width="141" height="81 src=">

имеет решения.

Решение. Ясно, что прямые семейства http://pandia.ru/text/78/074/images/image041_12.gif" width="61" height="52">..jpg" width="259" height="155">

Значение k1 найдем, подставив в первое уравнение системы пару (0;0). Отсюда k 1 =-1/4. Значение k 2 получим, потребовав от системы

http://pandia.ru/text/78/074/images/image045_12.gif" width="151" height="47"> при k > 0 иметь один корень. Отсюда k2 = 1/4.

Ответ. .

Сделаем одно замечание. В некоторых примерах этого пункта нам придется решать стандартную задачу: для прямой семейства находить ее угловой коэффициент, соответствующий моменту касания с кривой. Покажем, как это сделать в общем виде при помощи производной.

Если (х0 ; y 0) = центр поворота, то координаты (х 1; у 1) точки касания с кривой у = f (х) можно найти, решив систему

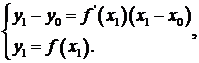
Искомый угловой коэффициент k равен .

Пример 6 . При каких значениях параметра уравнение имеет единственное решение?

Решение ..gif" width="160" height="29 src=">..gif" width="237" height="33">, дуга АВ.

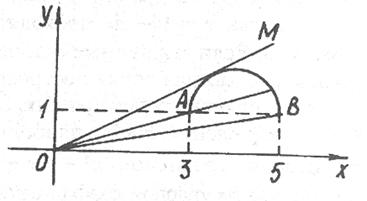
Все лучи проходящие между ОА и ОВ пересекают дугу АВ в одной точке, также в одной точке пересекают дугу АВ ОВ и ОМ (касательная)..gif" width="16" height="48 src=">. Угловой коэффициент касательной равен . Легко находится из системы

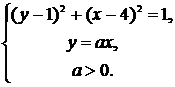
Итак, прямые семейства http://pandia.ru/text/78/074/images/image059_7.gif" width="139" height="52">.

Ответ . .

Пример 7 ..gif" width="160" height="25 src="> имеет решение?

Решение ..gif" width="61" height="24 src="> и убывает на . Точка - является точкой максимума.

Функция же - это семейство прямых, проходящих через точку http://pandia.ru/text/78/074/images/image062_7.gif" width="153" height="28"> является дуга АВ. Прямые , которые будут находиться между прямыми ОА и ОВ, удовлетворяют условию задачи..gif" width="17" height="47 src=">.

Ответ ..gif" width="15" height="20">решений нет.

1.3. Гомотетия. Сжатие к прямой.

Пример 8. Сколько решений имеет система

http://pandia.ru/text/78/074/images/image073_1.gif" width="41" height="20 src="> система решений не имеет. При фиксированном а > 0 графиком первого уравнения является квадрат с вершинами (а ; 0), (0;-а ), (-a ;0), (0;а). Таким образом, членами семейства являются гомотетичные квадраты (центр гомотетии – точка О(0; 0)).

Обратимся к рис. 8..gif" width="80" height="25"> каж­дая сторона квадрата име­ет две общие точки с ок­ружностью, а значит, сис­тема будет иметь восемь решений. При окружность окажется вписанной в квадрат, т. е. решений станет опять четыре. Очевидно при система решений не имеет.

Ответ. Если а < 1 или http://pandia.ru/text/78/074/images/image077_1.gif" width="56" height="25 src=">, то решений четыре; если , то решений восемь.

Пример 9 . Найти все значения параметра , при каждом из которых уравнение http://pandia.ru/text/78/074/images/image081_0.gif" width="181" height="29 src=">. Рассмотрим функцию ..jpg" width="195" height="162">

Число корней будет соответствовать числу 8 тогда, когда радиус полуокружности будет больше и меньше , то есть . Заметим, что есть .

Ответ . или .

1.4. Две прямые на плоскости

По существу, в основе идеи решения задач настоящего пункта лежит вопрос об исследовании взаимного расположения двух прямых: и . Несложно показать решение этой задачи в общем виде. Мы же обратимся непосредственно к конкретным характерным примерам, что, на наш взгляд, не нанесет ущерба общей стороне вопроса.

Пример 10. При каких a и b система

http://pandia.ru/text/78/074/images/image094_0.gif" width="160" height="25 src=">..gif" width="67" height="24 src=">, т..gif" width="116" height="55">

Неравенство системы задает полуплоскость с границей у = 2х – 1 (рис. 10). Легко сооб­разить, что полученная система имеет решение, если прямая ах + by = 5 пересекает границу полуплоскости или, будучи па­раллельной ей, лежит в полупло­скости у – 2х + 1 < 0.

Начнем со случая b = 0. Тогда, казалось бы, урав­нение ах + by = 5 задает верти­кальную прямую, которая оче­видно пересекает прямую у = 2х – 1. Однако это утверж­дение справедливо лишь при ..gif" width="43" height="20 src="> система имеет решения..gif" width="99" height="48">. В этом случае условие пересечения прямых достигается при , т. е. ..gif" width="52" height="48">.gif" width="41" height="20"> и , или и , или и http://pandia.ru/text/78/074/images/image109_0.gif" width="69" height="24 src=">.

− В координатной плоскости xOa строим график функции .

− Рассмотрим прямые и выделим те промежутки оси Oa, на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции http://pandia.ru/text/78/074/images/image109_0.gif" width="69" height="24"> в одной точке, в) в двух точках, г) в трех точках и так далее.

− Если поставлена задача найти значения x, то выражаем x через a для каждого из найденных промежутков значения a в отдельности.

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах..jpg" width="242" height="182">

Ответ. а = 0 или а = 1.

ЗАКЛЮЧЕНИЕ

Мы надеемся, что разобранные задачи достаточно убедитель­но демонстрируют эффективность предложенных методов. Одна­ко, к сожалению, сфера применения этих методов ограничена трудностями, с которыми можно столкнуться при построении графического образа. А так ли это плохо? По-видимому, нет. Ведь при таком подходе в большой степени теряется главная дидактическая ценность задач с параметрами как модели миниатюрного исследования. Впрочем, приведенные соображения адресованы учителям, а для абитуриентов вполне приемлема формула: цель оправдывает средства. Более того возьмем на себя смелость сказать, что в немалом числе вузов составители конкурсных задач с параметрами идут по пути от картинки к условию.

В этих задачах обсуждались те возможности решения задач с пара­метром, которые открываются нам при изображении на листе бумаге графиков функций, входящих в левую и правую части уравнений или неравенств. В связи с тем, что параметр может принимать произ­вольные значения, один или оба из изображаемых графиков движутся определенным образом на плоскости. Можно говорить о том, что получается целое семейство графиков, соответствующих различным значениям параметра.

Решительно подчеркнем две детали.

Во-первых, речь не идет о «графическом» решении. Все значения, координаты, корни вычисляются строго, аналитически, как решения соответствующих уравнений, систем. Это же относится к случаям касания или пересечения графиков. Они определяются не на глазок, а с помощью дискриминантов, производных и других доступных Вам инструментов. Картинка лишь дает путь решения.

Во-вторых, даже если Вы не найдете никакого пути решения задачи, связанного изображенными графиками, Ваше представление о задаче значительно расширится, Вы получите информацию для самопроверки и шансы на успех значительно возрастут. Точно представляя себе, что происходит в задаче при различных значениях параметра, Вы, возможно, найдет правильный алгоритм решения.

Поэтому эти слова завершим настоятельным предло­жением: если в хоть мало-мальски сложной задаче встречаются функции, графики которых Вы рисовать умеете, обязательно сделайте это, не пожалеете.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Черкасов, : Справочник для старшеклассников и поступающих в вузы [Текст] / , . – М.: АСТ-ПРЕСС, 2001. – 576 с.

2. Горштейн, с параметрами [Текст]: 3-е издание, дополненное и переработанное / , . – М.: Илекса, Харьков: Гимназия, 1999. – 336 с.

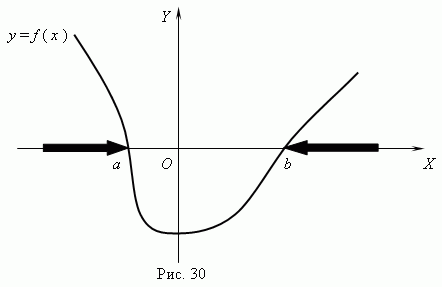
Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным , необходимо перенести все его члены в одну часть, т.e. привести к виду:

f (x ) > 0 ,

и построить график функции y = f ( x ). После этого, используя построенный график, можно найти нули функции , которые разделят ось Х на несколько интервалов. Теперь на основе этого определим интервалы x , внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции: a и b (рис.30). Тогда из графика очевидно, что интервалы, внутри которых f ( x ) > 0: x < a и x > b (они выделеныжирными стрелками). Ясно, что знак > здесь условный; вместо него может быть любой другой: < , .

Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т.e. привести неравенства к виду:

и построить графики функций y = f (x ), y = g (x ) , ... , y = h (x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т.e. их общую часть.

П р и м е р. Решить графически систему неравенств:

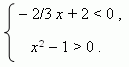
Р е ш е н и е. Сначала построим графики функций y = - 2 / 3 x + 2 и

y = x 2 -1 (рис.31):

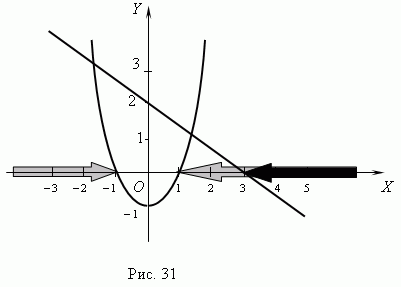
Решением первого неравенства является интервал x > 3, обозначенный на рис.31 чёрной стрелкой; решение второго неравенства состоит из двух интервалов: x < -1 и x > 1, обозначенных на рис.31 серыми стрелками.

Из графика видно, что пересечением этих двух решений является интервал x > 3. Это и есть решение заданной системы неравенств.

Чтобы решить графически систему двух неравенств сдвумя неизвестными, надо:

1) в каждом из них перенести все члены в одну часть, т.e. привести

неравенства к виду:

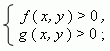
2) построить графики функций, заданных неявно: f ( x, y ) = 0 и g (x, y ) = 0;

3) каждый их этих графиков делит координатную плоскость на две части:

в одной из них неравенство справедливо, в другой - нет; чтобы решить

графически каждое из этих неравенств, достаточно проверить

справедливость неравенства в одной произвольной точке внутри любой

части плоскости; если неравенство имеет место в этой точке, значит

эта часть координатной плоскости является его решением, если нет - то

решением является противоположная часть плоскости ;

4) решением заданной системы неравенств является пересечение

(общая область) частей координатной плоскости.

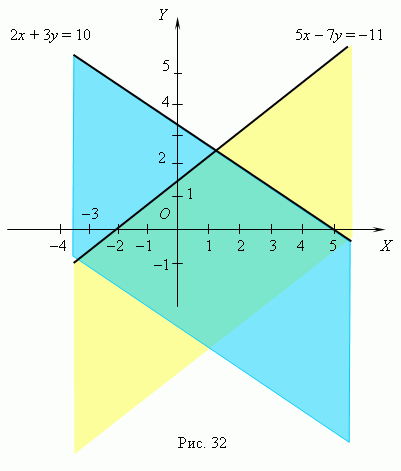
П р и м е р. Решить систему неравенств:

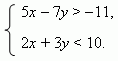
Р е ш е н и е. Сначала строим графики линейных функций: 5x - 7y = -11 и

2x + 3y = 10 (рис.32). Для каждой из них находим полуплоскость,

Внутри которой соответствующее заданное неравенство

Справедливо. Мы знаем, что достаточно проверить справедливость

Неравенства в одной произвольной точке области; в данном

Случае легче всего использовать для этого начало координат O (0, 0).

Подставляя его координаты в наши неравенства вместо x и y ,

Получим: 5 · 0 - 7 · 0 = 0 > -11, следовательно, нижняя

Полуплоскость (жёлтого цвета) является решением первого

Неравенства; 2 · 0 + 3 · 0 = 0 < 10, поэтому второе неравенство

Имеет своим решением также нижнюю полуплоскость (голубого

Цвета). Пересечение этих полуплоскостей (область цвета бирюзы)

Является решением нашей системы неравенств.